ORIGINS OF GEOMETRY

 HOW MATHEMATICAL CONCEPTS & GEOMETRY/TRIGONOMETRY ORIGINATED FROM THE CIRCLE.

In my previous posts. I have demonstrated how ancient civilizations could draw circles using mathematical apparatus and readily available. Thus, they could draw the circle, the seed of life, the fruit of life, the tree of life, and other sacred geometrical shapes beyond the three. This page is dedicated to showing how and why the circle is the basis of the basic mathematical concepts, geometry, and trigonometry.

The Seed of Life

The above image shows the basic version of the seed of life. This above image is of great significance as is the foundation of geometry and trigonometry. The following illustrations show why this simple shape is the foundation of all we know about mathematics and metrology.

The Circle

The first significance of the seed of life is that it was the first perfect shape or geometrical shape that could be drawn even thousands of years ago.

The circle: The Gregorian Universal Systems & Units of Measurements System (GUSUMS) argues that the circle is the basis and origin of metrology and mathematics as it was the first perfect shape that could be drawn by any civilization. Thus, with just a rope and 2 sticks, or just a stick as explained in the origin of metrology the circle was discovered and it is from this that all other geometrical shapes can be created.

Radius, Diameter, Linear Measurements, Distance, & First System & Units of Measurements.

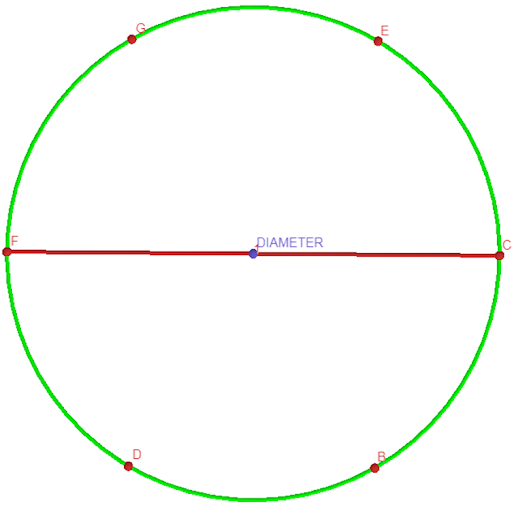
With the circle or the seed of life, the concept of the radius of a circle was discovered as each of the leaf-like shapes is equal and thus each one is half the full length of the distance across the circle. This is even more important as it was the basis of;

1.      Linear measurements: Linear measurements refer to the measure of the gap between two straight points or points on the same axis. Thus, with the seed of life ancient civilizations were able to connect 2 or more points.

2.      Distance: With a line it was possible to measure the length of space between two points which is the distance.

3.      Units of Measurements & Values: Note that this did not even require mathematical descriptions or knowledge of numbers as it could be expressed as half of something even in sign language or in relation to objects. For example, half a foot, palm, stick, finger, etc. That is why GUSUMS on the origins of length states that the foot is not a measure of an object but a ratio. Thus, it was this comparison of properties of objects in relation to others that resulted in the formation of measurement systems. This is why ideally, 1 inch should be equal to 2.5cm and not 2.54cm.

4.      Diameter: The distance across any of the corresponding 2 points of the circle resulted in the creation of the diameter as shown below. Thus, the diameter could be expressed in relation to the radius without numbers. For example, the diameter could be expressed as a full stick, palm, finger, foot, etc. if the radius was half a stick, foot, palm, finger, etc. This further confirms that the units of measurement were based on ratios and not materials. As GUSUMS suggests, the ratio should not be ‘made up’ figures based on objects but constant values that can perfectly divide the circle.

Circular Measurements & the First Concept of Pi

1.      Circular Measurements: GUSUMS in the origins of distance measurements defines circular measurements as the measures of curves and circular values. Before ancient civilizations could understand, invent, or improve number measurements, they relied on how objects relate to each other to describe distance as explained above. Based on this, we can assume that the first diameter of the first circle was either 1 foot, arm, palm, feet, leg, body, stick, tree, rope, etc. Thus, in measuring the circumference of the first circle, they could have used a rope that goes around a circle to measure the circumference of the circle and relate it to the ratio of its diameter or radius. This means, that assuming the Diameter of the first circle was 1 palm, foot, stick, rope, or body length, then the circumference of the circle would be the number of palms, feet, sticks, ropes, or body length that covered the entirety of its circumference. Thus, this was the basis of the first circular measurements and its value.

2.      Origins of Pi: So what is the circumference of a circle with a diameter of 1? The answer is PI!!!

The above shows that the radius of any circle with a diameter of one will always have a circumference that is pi times that particular unit. As simple and as obvious as this explanation might seem it can immensely influence our current units of measurement based on the following implications:

       I.            It disagrees with Archimedes on the value of pi as Archimedes stated that the value of pi varies in the ratio of 223/71 < π < 22/7 or with an average ratio of 3.1418, GUSUMS or the GUSUMS pi on the earth hand, states that pi is a constant.

 

    II.            This means that by using Archimedes Pi our current calculations are wrong. This means that we do not have the correct values of the orbits, diameters, radius, circumferences, area, aphelion, orbital days, perihelion, distance from the sun, orbital days, rotational days, etc. of all the planetary objects. As proof of this, GUSUMS has provided images and a table of the origin of pi as evidence of the pi being a constant.

 

 III.            This means that the exact value of pi I is 22/7 or 3.142857142857142857….and cannot have any other value.

 

Direction

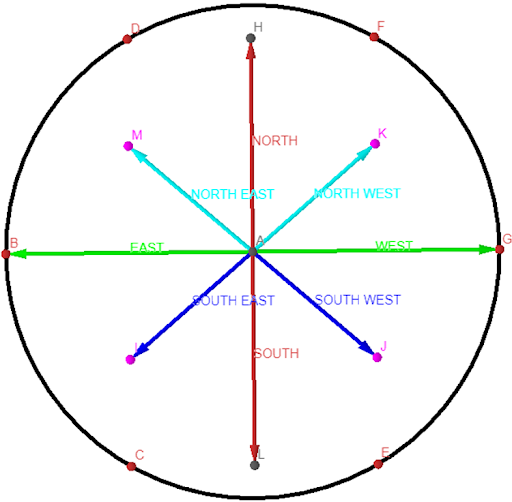
The Cambridge Dictionary defines directions as the position towards which someone or something moves or faces:. From the circle, it was possible to describe direction based on the center of the circle. For example, point  E is below A or point D is above A. This is the foundation of compass points direction and navigation. I have enhanced the visualization of these concepts by adding the additional midpoints in which the circles intersect in the seed of life to show the exact compass points that we use today as shown below.

Axis of the Circles: The above image is also where the concept of the axis originated from. The original axes are X, Y, and occasionally the Z axis. However, we can still Improve on this by adding additional axes using the compass points as a basis. The image below shows the 3 basic axes as they could be created by just using the seed of life.

ORIGINS OF BASIC GEOMETRICAL SHAPES

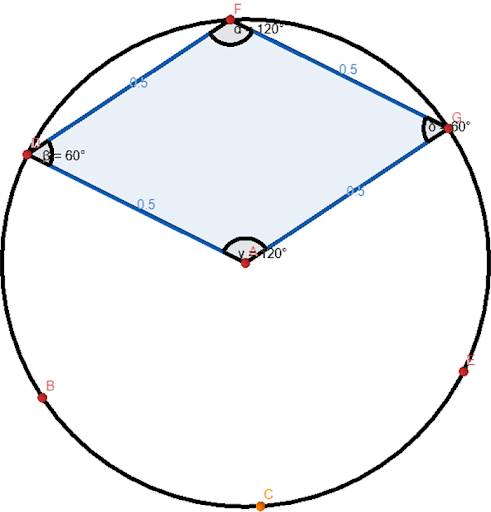
Geometry and geometric shapes originated by joining points of the circle in which 2 or more circles intersect. I have added additional measurements to show that this could be done with the highest level of accuracy.

Triangles

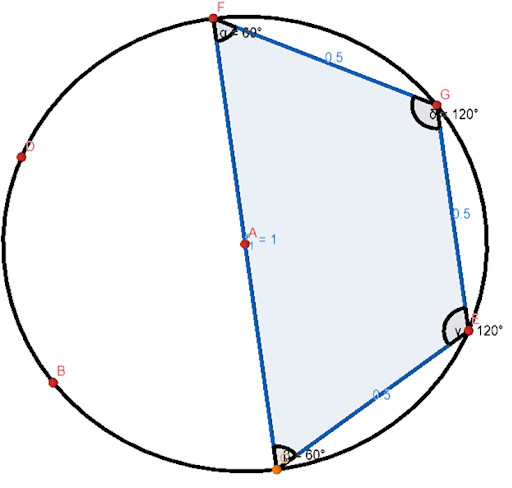
1.      Equilateral Triangles: All sides are equal and all angles are also equal or 360 degrees

1.      Right Angle Tringles: One of the sides is 90 degrees.

1.      Scalene Triangles: All angles  and sides are not equal.

1.      Acute Triangles: All angles are less than 90 degrees.

1.      Obtuse Triangle: One angle is more than 90 degrees

1.      Isosceles Triangles: Two of the angles are equal.

·         Obtuse Triangle: One angle is more than 90 degrees.

 

Quadrilaterals

Rectangle: All angles are 90 degrees and opposite sides are equal.

Parallelogram: All sides are equal, opposite angles are equal

Trapezium

Other Shapes

Hexagon

3D SHAPES

Cube: All sides and angles are equal or squares

Tetrahedron/Pyramid

 

The Concepts of Mathematical Operations

Another significance of the Seed of Life is that it introduced humanity to concepts of mathematical operations such as divisions and additions.

Addition: Adding 6 circles from the original circle created the seed of life.

Division: By adding additional circles, humans were able to divide the circle perfectly into 6 equal parts as shown below.

More concepts of the above is explained in the origins of metrology

Concepts of Rotation & Revolution

Rotation: By going to one end of the circle and drawing additional circles was the origin of the concept of rotation.

1.      Initial circle

Rotations of the circles

Revolution: From the rotation of the circles, continuing with the same steps of going to where two or more circles intersect and drawing additional circles until another circle perfectly rotates or revolves around the first circle without actually touching it or interfering with it was the origin of revolution. A complete Revolution is depicted below.