ORIGINS OF ANGLES
The Gregorian Universal
System and Units of Measurement System (GUSUMS) also provides illustration that
shows that angles originated from the circle. This starts with the circle which
is the first perfect geometrical shape that could be as explained by GUSUMS in
the origins of geometry and the origins of numbers and numbering.
The Circle-Angle 360 degrees
Since the total angles
in a triangle are equal to 360 degrees, this was the origin of angles.
 |
| Angles in a circle |
The seed of life
From the circle, other
angles could also be created based on the subsequent divisions of the subsequent
sacred geometrical circles. The first circular sacred geometrical shapes that
can be created after the circle is the seed of life. Which divides the circle into 6 equal parts
 |
| The seed of life divides the Circle into 6 equal parts |
Angles 60
Since the seed of life divides
the circle into equal parts and the total number of angles in a circle is equal
to 360 degrees, then each division of the seed of life is 60 degrees. This,
explains the origins of the 60 degree and how humanity was first able to create
it.
 |
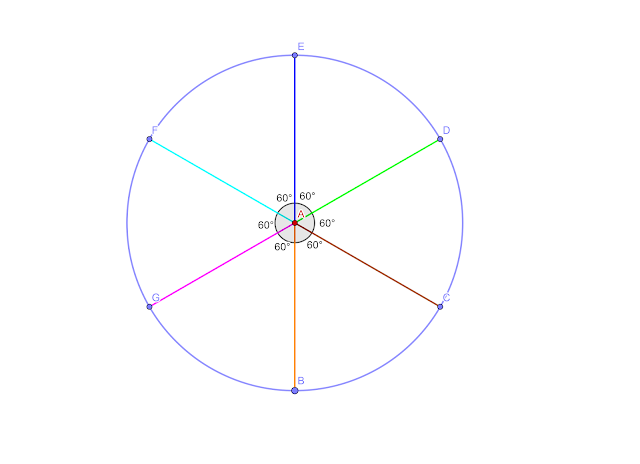| 60 degrees angles derived from sacred geometry in the seed of life |
Angle 120
Combining 2 of the 60
degrees angles creates an angle that is 120 degrees.
 |
| An angle of 120 degrees derived from the circle |
Angle 180
Combining 3 of the 60
degrees angles divides the circle into 2 equal parts. This means that each
angle will be 180 degrees.
 |
| An angle of 180 degrees |
Angle 240
Adding an additional 60
degree angle in the fruit of life creates an angle that is 240 degrees.
 |
| A 240 degrees angle |
The Second Circular Shapes
From the seed of life,
the next circular sacred geometrical shape that can be formed contains 12
divisions.
 |
| The second circle with 12 divisions |
Angles in the Second Circle
Since each division
from the center is equal, then each angle is equal to 360 divided by 12 or 30
degrees Thus, from the second circle it is possible to create angles of 30
degrees, 60 degrees, 90 degrees, 120 degrees, 150 degrees, 180 degrees, 210
degrees, 240 degrees, 270 degrees, 300 degrees, 330, degrees, and 360 degrees.
The Third Circle
The third circle
divides the circle into 18 parts.
 |
| The Third Circle is the fruit of life with 18 divisions |
Angles of the Third Circle
Angles in the third
circle are not all equal as it comprises of angles that are 19.1 degrees and
angles that are 21.8 degrees.
 |
| Angles in the fruit of life |
The Origins of Angles Summary
From the above, we can
conclude that angles originated from the circle based on the number of
divisions of the circle. We also know that the number of divisions increases
based on multiples of 6. This is because the first circle had 6 divisions, the
second has 12 divisions, the third has 18, the fourth has 24, and so on and so
forth. Thus, GUSUMS is right for concluding that angles originated from the
circle as using the circle all angles can be created from all multiples of 6
that are in 360. In addition, the above illustrations also show that we can
combine various numbers of angles to create additional angles other than the
ones gotten from the multiples of 6 e.g by combining two 60 degrees angle to
create 120, or combining 3 30 degrees angle to create a 90 degree angle. So, essentialy any angle can be
created from the circle. Thus, based on the divisions of the circle we can
create angles containing any combination of the following multiples of 6 that
can divide 360.
Link to the Book: The Gregorian Universal System and Units of Measurement System (GUSUMS): The Art of Mathematics
No comments:
Post a Comment