The Correct Value of Pi and the GUSUMS Formula for Calculating the Circumference of the Circle
A new mathematical discovery
made by Isaac Gregory Odhiambo, is the GUSUMS formula for calculating the
circumference of a circle. The GUSUMS formula for calculating the Circumference
of a circle is
CIRCUMFERENCE =
DIAMETER*3 + DIAMETER/7
 |
| The GUSUMS formula for calculating the circumference of a circle |
The above formula shows
that the value of pi is exactly 22/7 and that it does not vary as previously
thought. If this is true then our current value of pi is off by 0.04024994348%.
This implies that our current circumference of the sun is off by about 1093.7
miles or 1758.9 KM. This also means that the current value of the circumference
of the earth is off by about 10 miles or 16 km. This further translates to other
measurements that are dependent on pi in astronomy, astrophysics, and metrology (the study of measurements) such as the orbital days of planets, units of time, mass, radius, aphelion,
perihelion, velocity, speed, gravitational pull, temperature, etc., that depend
on the current value of pi or distance estimation might also be wrong. Thus, it
is indeed important to highlight and illustrate the origins and justification
for the GUSUMS pi and the resultant formula for calculating the circumference
of the circle.
The Definition of Pi: What is Pi?
The most common
definitions of pi is that pi is a mathematical constant that is the ratio
of a circle's circumference to its diameter.
GUSUMS has redefined pi to the circumference of a circle with a diameter
of 1 and a radius of 0.5. This is because in whatever units one measures the
circumference of a circle with a diameter of one unit and a radius of 0.5 unit,
the circumference will always be equal to pi units. This explains why almost
all ancient civilizations had an almost equal value of pi despite limited
interactions or when using different units.
 |
| The Default value of pi |
The Value of Pi
One item that GUSUMS,
the current value of pi, the ancient Babylonians, the ancient Egyptians, and
Archimedes disagree on is the exact value of pi. GUSUMS states that pi is
exactly 22/7, Archimedes approximated the value of pi to be between 223/71
& 22/7 with an average value of pi is 3.1418, ancient Egyptians
approximated the average value of pi to be equal to about 3.16045, the
Babylonians approximated the value of pi to be approximately 3.125, and our current value of pi is
approximately 3.14159.
So, who is right?
Origins of Pi
Perhaps the most detail explanation an justification of pi comes from Archimedes’ approach. Archimedes identified the value of pi by circumscribing a circles around hexagons and identifying the relationship between the circumference of the circle and the perimeter of the hexagon. GUSUMS also adopted the same approach as Archimedes. However GUSUMS noted that the accuracy from the Archimedes calculations might have been limited to the technology and knowledge at the time. As a result, GUSUMS also utilized the current definition of the pi as the ratio of the circle’s diameter and its circumference. From this GUSUMS was able to create a formula that combines both of the two. Thus, the GUSUMS Pi consist of the ratio of the circle’s diameter and its circumference (Diameter divided by 7) and the relationship between the perimeter of the hexagon and the circumference of the circle (Diameter multiplied by 3) to maximize on the best of both worlds. To further enhance the formula GUSUMS also utilized the concept and discoveries made regarding circular and linear measurements to justify the final figures.
Origins of the GUSUMS formula for Calculating the Circumference of a Circle
The Seed of life
 |
| The seed of life |
In sacred geometry, the
first rotation results in the formation of the seed of life. The seed of life
divides the original circle into 6 equal parts
 |
| Measures of the seed of life |
The Default values of the Seed of Life
As the first circle, the
seed of life has the default values. This means each radius is 0.5 units, the
diameter is 1 unit, and the circumference is equal to pi.
 |
| Default values of the seed of life |
The First Hexagon
Since, the first
perfect divisions is equal to 6 parts, then it goes without saying that the
first polygon that can be formed is the hexagon.
 |
| The hexagon drawn from the seed of life |
Measurements of the First Hexagon
The first hexagon will thus
have sides that have equal measurements as the radius of the circle. This means
that each side will be equal to the radius or 0.5 units and the perimeter will
be equal to 3 units. From this we can observe that the relationship between the
diameter of the circle and the perimeter of the hexagon is that the perimeter
of the hexagon is 3 times the diameter. The value of the circumference is pi.
 |
| Measurements of the first hexagon |
The Second Hexagon
The second circle can
be formed when the number of divisions are 12. This results in a radius of 1, a
diameter of 2, and the perimeter of the hexagon and circumference of the circle
also doubles.
 |
| Measurements of the second Hexagon |
The Third Hexagon
The third hexagon also
repeats the same pattern as the radius, diameter, perimeter, and circumference
also triples.
 |
| Measurements of the third Hexagon |
The Fourth Circle
The fourth Circle is
not an exception as the perimeter of the hexagon also is 4 times the original
perimeter of 3.
 |
| Measurements of the fourth hexagon |
From the above, GUSUMS
noted that the perimeter of the hexagon is always 3 times the diameter and
hence the Origins of;
DIAMETER*3
Circumference of the Circles
The circumferences of
the circles are shown below.
 |
| Circumferences of the circles |
The Second Component
From the above, we can
note that the relationship between the perimeter of the hexagon and the circle
or its circumference. That is the perimeter of the hexagon is always thrice the
diameter. Thus, the remainder is the relationship between the diameter and the
circumference of a circle.
 |
| Table showing the linear component and the remainder |
Factors of 7
GUSUMS, noted that the
remainders are almost equal to factors of 7 which are shown below.
Furthermore. From the
discussions on linear measurements, GUSUMS had noted that linear measurements
entail the perfect divisions of the circle. Thus, using the number of degrees
in a circle as a basis, GUSUMS had summarized that linear units can be defined
by the natural numbers that are factors of 360-1, 2, 3, 4, 5, 6, 8, 9, 10, 12,
15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 and 360.. This means
linear measurements can be allocated the following factors and their subsequent
multipliers as shown below.
From one to 10, a
notable absentee is 7. Thus, if 7 is not a linear factor then it is likely to
be circular. Furthermore, a key characteristic of linear factors is that their
multiplier tend to have repeating digits of the same subsequent unit which the
multipliers of 7 do not adhere to. Hence
the GUSUMS formula of;
CIRCUMFERENCE =
DIAMETER*3 + DIAMETER/7
Confirmation of GUSUMS
Pi
It is important to note
that the above values of the circumference of the circle was based on the
current value of pi (y^2 + X^2 = R^2) where are is the radius. To confirm the
value of pi using the GUSUMS formula, GUSUMS tested if perfect circles can be
formed when (y^2 + x^2 = D*3 + D/7) where D is the diameter.
 |
| Circle formed using the GUSUMS formula when the diameter is 1 |
 |
| Circle formed using the GUSUMS formula when the diameter is 2 |
 |
| Circle formed using the GUSUMS formula when the diameter is 3 and the circumference |
 |
| Circle formed using the GUSUMS formula when the diameter is 4 and its resultant Circumference |
 |
| Circle formed using the GUSUMS formula when the diameter is 5 and its resultant Circumference |
 |
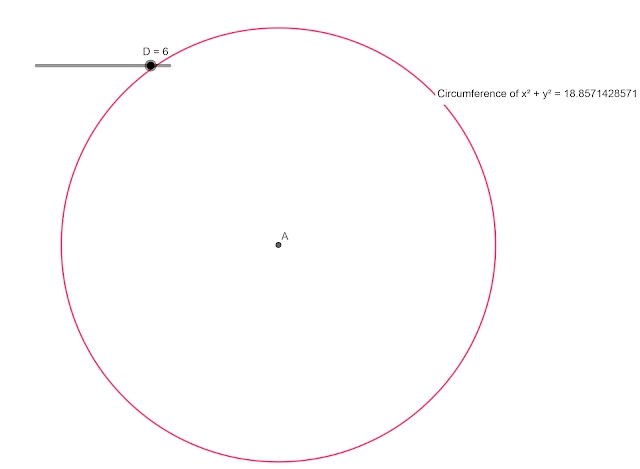| Circle formed using the GUSUMS formula when the diameter is 6 and its resultant Circumference |
 |
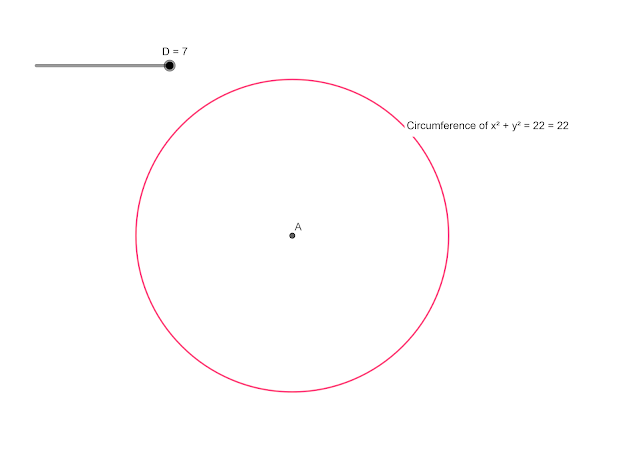| Circle formed using the GUSUMS formula when the diameter is 7 and its resultant Circumference |
All the above point out to the possibility of pi being exactly 22/7!
No comments:
Post a Comment