Numbers

 

The Origins of Number and Numbering

Link to the Book: The Gregorian Universal System and Units of Measurement System (GUSUMS): The Art of Mathematics

According to the Gregorian Universal System and Units of Measurement System (GUSUMS), numbers, numbering, multiples, multipliers, units, conversions, etc originated from the circle. GUSUMS states that this was not based on mathematical calculations but the flow of sacred geometrical shapes that created divisions of the circle.

Origins of Factor and Multiple

The key items when it comes to numbers and numbering are the concepts factor and multiples. A factor is a number that divides into another number exactly with no remainder. This implies that a factor is the number of sub-units in a particular units. This is represented by the dot in sacred geometry. A multiple is a number that can be divided by another number without leaving a remainder. This implies that a multiple is the unit in a particular system. In sacred  geometry, this can be represented by a circle.

The concept of factors and multiples from sacred geometry

The original Circle

Thus, the first circle is the original circle

The Original Circle

Number of Factors in the Original Circle

To get the number of factors or the multiple of a particular unit, we need to identify the number of factors that fit in a particular circle or the subsequent unit of measurement. To do this, we move to any point on the circumference of the original circle such as point B in the diagram below.

Point B marks the start of identifying the number of factors of the first unit or the number of sub-units in the first circle

First Circle

The point B above thus represents a single sub-unit or factor. To get the exact number of factors that fit in the first unit of measurement represented by the first circle, we need to create additional circles from point and rotate around the circle until we get back to B. Thus, from the point B, we can draw another circle with its center being point B and its radius being AB as shown below with the point B represented a single unit of the factor.

The first Circle

Second Circle

The point B represents a single unit and the goal is to rotate around the original unit and back to B. We can also note that point B create 2 additional intersection. Thus, we can label the point to the left of B as Point C. As the goal is to rotate around the original circle, we can then draw another C from point. The center of this circle will be point C and its radius will be from point C to point A. The images below illustrate this.

point C

The Second Circle

The Third Circle

From the circle drawn from point C, we can highlight the point D as our goal is to rotate around the original point. From point D we can draw another Circle with its center being point D and its radius being AD as illustrated below.

Point D

The third Circle

The Fourth Circle

From the circle drawn from point D, we can highlight the point E as our goal is to rotate around the original point. From point E we can draw another Circle with its center being point E and its radius being AE as illustrated below.

Point E of the circle

The Fourth Circle

The Fifth Circle

From the circle drawn from point E, we can highlight the point F. From point F we can draw another Circle with its center being point F and its radius being AF as illustrated below.

Point F

The 5th Circle

The Sixth Circle

From the circle drawn from point F, we can highlight the point G. From point G we can draw another Circle with its center being point G and its radius being AG as illustrated below.

Point G

The 6th Circle

 

Multiples and  Factors of Units

The First Multiples and Units- 6 units

The first 6 circle show that the first circle contains 6 factors of the original circle. Thus, the first units of measurements can be divided into 6 units of the smallest units of measurements.

First Unit Contains 6 factors

The Second Multiples and Units-12 units

From the above, we can note that each circle represents a unit of measurement. Thus, we can replicate the same process by identifying the subsequent intersecting points of the circles from the original circle and drawing additional circles.  From that, we can identify the subsequent units by identifying areas in which a perfect circle can be formed. Having done this the second circle is formed when the radius of the original circle is doubled. This implies that the second multiple of measurement has 12 factors of the original circle.

12 sub-units/sub-divisions in the second circle

The Third Multiples and Units-18 units

The third circle forms when the radius and the diameter of the original circle triples. The number of points in this circle is 18. This implies it contains 6 factors of the smallest unit.

18 sub-units or divisions in the third Circle

The Fourth Multiples and Subsequent Circles

The next circle formed has 24 units or factors of the smallest units of measurement. The one that comes after has 30 units and the pattern continues to infinity.

The pattern Divisions of the Circles

From the above, we can identify a pattern in that each subsequent unit increases by 6 factors. From this we can create a pattern that summarizes the first 12 divisions as follows.

Translation to Units of Measurements

To show that the above is true, the following are some of our current units that follow the pattern

PALM   FATHOM 1 = 0.041666666666667

INCHES   LINK (RAMSDEN'S; ENGINEER'S) 1 = 0.083333333333333

PALM   YARD 1 = 0.083333333333333

INCHES   PACE 1 = 0.033333333333333

INCHES   YARD 1 = 0.027777777777778

Rod   Inches 1 = 0.00505050505050

FOOTS   Hand 1 = 0.033333333333333

Chain   Hand 1 = 0.005050505050505

Furlong   YARD 1 = 0.33333333333333

PALM   FINGER (CLOTH) 1 = 0.66666666666667

INCHES   FOOTS 1 = 0.083333333333333

FOOTS   YARD 1 = 0.33333333333333

Minutes   Seconds 1 = 0.0166666666667

Hours   Minutes 1 = 0.0166666666667

Days   Hours 1 = 0.0466666666667

Hours   Seconds 1 = 0.00027777777777778

Decameter   Nautical Miles 1 = 0.001851851851852

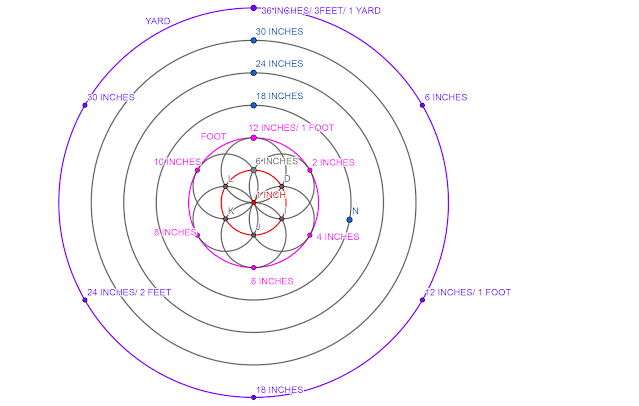
 Using the  imperial systems of length we can observe this pattern if we take the inch as the smallest unit

Imperial units of measurement as an example
Link to the Book: The Gregorian Universal System and Units of Measurement System (GUSUMS): The Art of Mathematics