Origins
of Length and Linear Measurements
The
Gregorian Universal System and Units of Measurement System (GUSUMS) was also
able to derive the units of length from the circle. With this, GUSUMS was able
to derive the both the imperial and metric units from the circle and provide a
means of unifying the two as discussed below.
The key elements in Length Measurements
When
it comes to measuring length and assigning units, the key items are the factors
and multiples of length and their value. A factor is a number that divides into another number exactly with no
remainder. This implies
that a factor is the number of sub-units in a particular units. This is
represented by the dot in sacred geometry. A multiple is a number that can be
divided by another number without leaving a remainder. As earlier stated, GUSUMS showed that a multiples are represented by the circle and factors by the number points in circular sacred geometrical shapes.
 |
| The circle represents multiples, and the point represents factors. |
Multiples and Factors of length
To get the first multiples of length as
explained in the origins of numbers and numbering, we move to any point in the
circle and draw a circle whose center will be the point of the identified circle and radius will be the distance from
the center of the original circle above to the identified point. From that, we
can move upwards and rightwards by drawing subsequent points on the subsequent
intersection of the resultant circles as shown below.
Point C
.png "point C") |
| Point C of the original circle |
Circle From Point C
From the point C of the original circle, we can draw a circle as shown below.
Circle From Point D
 |
| Circle drawn from point D |
Circle From Point E
The circle drawn from point D above, creates another intersection. To the right of point D is the point E. Going to point E, we can create another circle whose center will point E and whose radius will be from E to the center of the original circle.
 |
| Circle drawn from point E |
Circle from Point F
We can then move to the right of point E and draw another circle whose center will be point F and the radius will be from F to the center of the original circle.
 |
| Circle drawn from point F |
Circle From Point G
The circle drawn from point F creates the intersection at point G. Thus, we can move to point G and draw another circle whose center will be G and the radius will be from point G to the center of the original circle whose center point represents the smallest unit of measurement.
 |
| Circle Drawn From Point G |
Circle from Point H
We can finally go to point F that is created from the circle drawn from point G and complete the number of divisions of the original circle.
 |
| Circle drawn from point h |
Multiples and Divisions of Units of Length
First Unit of length
From the above process, we can see that the first unit of
length has 6 factors or equal divisions.
 |
| The First Unit of Length has 6 factors |
Second Unit of Length
To get to the second unit of length, we replicate the same
process by going to the outer intersections of the circles and drawing
additional circles. From that, we identify the next unit of length by
identifying the next point of intersection where another circle that can be
formed around the first multiple of length. The shape below shows the position
of the next unit of length which has 12 divisions
 |
| The 2nd unit of length has 12 divisions of factors. |
The Third Unit of Length
By continuing the same process, we can see that the third
unit of length forms when there are 18 divisions.
 |
| The third Unit of length has 18 divisions or factors |
The Fourth Unit of Length
The Fourth Unit of length forms when the number of divisions
is equal to 24.
 |
| The Fourth Unit of length has 24 divisions |
The Fifth Unit of Length
The fifth Unit of length forms when the number of divisions
of the circle is equal to 30 divisions or factors.
 |
| 30 divisions of the 5th unit of length |
The Sixth Unit of Length
The 6TH Unit of length then forms when the total
number of divisions is equal to 36 divisions.
 |
| The 6th Unit of length has 36 divisions |
Table of Length
From the above, we can see that the sub-division of length is
based on multiples of 6. From this, we can create a table to reflect this.
Using the number of degrees as a basis, we can show the first 60 divisions/
units of length and their multiples and factors as shown below.
Origins of the Imperial System
The main units of length in the imperial system are; inches,
feet, yards, and the mile. Other Units include; the palm, the finger, cloth, furlong,
and rod. Using the inch as a basis, the conversion of the other units to inches
is as follows;
 |
| The first 60 multiples of length and their multipliers |
Deriving the Metric and Imperial Systems From the Divisions of the Circle
The Imperial System
 |
| Imperial units of length conversion to inches |
From the above table, we can create a metric table showing
the conversion of all the above units as shown below.
 |
| Conversion table for imperial units of length |
From the above table, we can note that the multipliers of the imperial system of measurements have similar multiples to the table of divisions of the circle. For instant, we can allocate a unit such as the inches to the first point in the original circle and identify the rest based on the multipliers or factors. For example, assuming the inch is the first point, then the foot and yards can be allocated or based on other circles and divisions as follows.
 |
| Deriving units in the imperial system from the circle |
The above shows that all the metric units of measurements are
based on the division of the circle. Note that some of the units are not visible
as the number of divisions of the circle was limited to 360 divisions. However,
the main idea is that imperial system is based on the division of the circle.
Origins of the Metric System
The table below shows the basic metric system of measurements.
 |
| Conversion of metric units |
Deriving the Metric System.
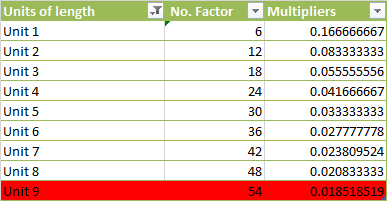
The metric system can also be derived from the table containing the multiples and multiplies of the divisions of the circle. To do this we can use the Nautical miles. From what we know, one nautical mile is approximately 1.852 km. From the table of divisions of the circle, We can note that the 9th circle has 54 divisions and a multiplier of 0.0018515151.
This implies that this is the conversion of the nautical mile to
the decameter. Thus, using this figure we can note that a nautical mile is not
exactly 1.852 but it is actually 1.85151515151515. From this, we can identify
the other units in the metric system using the nautical mile.
 |
| Deriving metric units of length using the nautical mile |
From the above explanations, we can note that both the metric and imperial system originated from the circle. This entailed the division of the circle into equal parts without leaving any remainders.
Link to the Book: The Gregorian Universal System and Units of Measurement System (GUSUMS): The Art of Mathematics
No comments:
Post a Comment